1.2: Models, Goals, And Learning
08 Sep 2017
What Is Intelligence, Really???
“I keep trying to explain to people that the archetype of intelligence is not Dustin Hoffman in ‘The Rain Man’, it is a human being, period.” — Eliezer Yudkowsky
There’s a lot of complex factors involved in intelligence. Just holding a conversation involves a plethora of flexible, general skills: task prioritization, abstract reasoning, synthesizing relevant information, and maybe even creativity … Yet despite all this, intelligence can be summarized in just three words.
Goal-directed behavior.
Whether it’s driving a car or designing rockets, making small talk or inspiring nations, musing about yesterday’s lunch or introspecting on the meaning of life — all the multifaceted, dizzyingly intricate behaviors that we exhibit are in furtherance of our goals and values. Some of these goals are implicit, some are explicit, but they are always there. We think because we care; otherwise, why even bother?
We define artificial intelligence in much the same way as the real kind; programs that effectively work towards accomplishing their goals. Ultimately, the only AI worthy of the moniker “intelligent” is one that succeeds.
The Rollercoaster Test
Successful AI programs tend to involve three main components: modeling, goal evaluation, and learning.
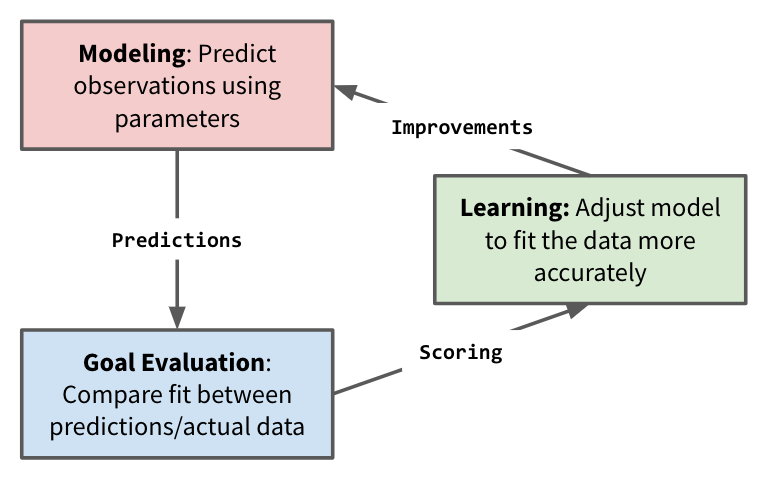
Understanding this paradigm is central to learning to write useful deep learning code — in fact, we’re probably going to use it in every program in this course. So, for practice, we’ll start with an example that’s both (laughably) simple and (hopefully) memorable.
Yeah, you guessed it. We’re going to try and predict whether a given person, with height H, can get onto a rollercoaster. Using a “dataset” composed of the fortunate people who got in … and the vertically-challenged people who didn’t make it.

Hello, my old friend.
There’s probably a number of questions that are running through your mind right now. Like, “In what vanishingly strange, speculative scenario would this be useful?” Or, “Why not just walk up to the sign and look at it?”. *Or, *“Is it possible to get a refund on a free online course?”
But in time, all your questions will be answered. In time, you’ll learn what every true AI researcher knows: the simple pleasure of forcing smart computers to do very stupid things.
So pull up Python, open a new file and let’s get to coding!
Modeling
“All models are wrong, but only some are useful.” — George Box
The first thing every AI needs is some sort of model of the world around it. An initial hypothesis about the nature of the data that it manipulates. This model doesn’t need to be right, or even close to right. However, it does need to have the possibility of being adjusted and modified to correctness.
Every task requires its own unique type of model. For example, a geographical map would be useful for a self-driving car, but far less useful for a music generation engine.
For this specific problem, our model is absurdly simple. It is parametrized by a single value, $H$, and predicts that people will only be let on the rollercoaster if they are taller than the threshold ($h \geq H$).*
# Returns predictions for array of input heights
def predict(H, data):
return [height > H for height in data]
Goal Evaluation
“Intelligence without ambition is a bird without wings.” — Salvador Dali
Every machine learning task involves goals. Some goals are all-or-nothing, but for most objectives it is entirely possible to make steady progress towards success, without necessarily reaching it. Evaluation metrics give you a measure of this progress.
For this specific task, our goal is simple: correctly predict whether various children are allowed on the rollercoaster. We need a dataset of examples, as well as a simple Python function to measure our prediction accuracy for each value of $H$.
# We definitely did not make up this data on the fly
# It was collected through rigorous experimentation
heights = [20, 35, 42, 45, 46, 49, 60]
allowed = [False, False, False, True, True, True, True]
# Evaluates and returns the current model accuracy
def evaluate(H):
predictions = predict(H, heights)
num_correct = 0
for prediction, target in zip(predictions, allowed):
if prediction == target: num_correct += 1
accuracy = 100.0*num_correct/\len(allowed)
return accuracy
Learning
The last and final step we need is the learning phase, in which our model is iteratively corrected to become more and more accurate. Learning is always finicky: you need to strike a balance between exploration — trying a bunch of diverse model configurations — and exploitation — homing in on one specific configuration that works well.
In this specific case, the state space is so small that we can use a simple uniform search to find the optimum threshold $H$. We just start at the lowest possible threshold ($0$) and increase by increments of ($1$), recording the value of $H$ that achieves the highest accuracy.
best_H = 0
best_accuracy = 0.0
for H in range(0, 100):
accuracy = evaluate(H=H)
print (H, accuracy)
if accuracy > best_accuracy:
best_accuracy = accuracy
print ("Best threshold: ", best_H)
print ("Best accuracy: ", best_accuracy)
Putting It All Together
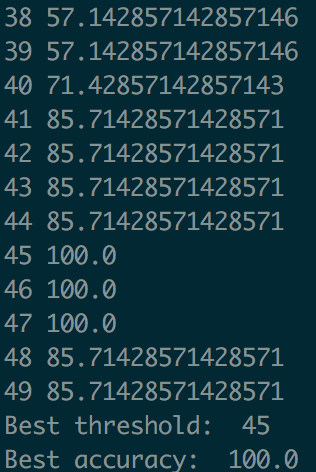
We can now run our program and use it to find the optimum value of $H$ — that is, the threshold value that fits the dataset the best. This results in a “model” that can easily predict whether new riders will be allowed on the rollercoaster or not.
# Returns predictions for array of input heights
def predict(H, data):
return [height > H for height in data]
heights = [20, 35, 42, 45, 46, 49, 60]
allowed = [False, False, False, True, True, True, True]
# Evaluates and returns the current model accuracy
def evaluate(H):
predictions = predict(H, heights)
num_correct = 0
for prediction, target in zip(predictions, allowed):
if prediction == target: num_correct += 1
accuracy = 100.0*num_correct/len(allowed)
return accuracy
best_H = 0
best_accuracy = 0.0
for H in range(0, 100):
accuracy = evaluate(H=H)
print (H, accuracy)
if accuracy > best_accuracy:
best_accuracy = accuracy
best_H = H
print ("Best threshold: ", best_H)
print ("Best accuracy: ", best_accuracy)
It works! We find that using a threshold of 45, we can get 100% accuracy in predicting who will be let on the coaster.